Three interviewers A,B, and C | GMAT | Quant | Overlapping Sets | Hard | Official Question

Question Details

Note: Because of copyright, we are not showing the full question here. You can use the following GMATClub link to access the question and solve it for yourself, before reading the solution below.

Link to the question on GMATClub: Here

Solution

As is true with many GMAT Quant questions, this is a logical reasoning problem masquerading as a math problem!

You could solve this question by drawing Venn diagrams. You could also make a bunch of algebraic equations and eventually arrive at the correct answer.

But what if I tell you that this question can be solved without either of the above?

Here is an interesting way to solve this question ->

1. We know that there are 40 applicants in total. We are also given that a total of 15 applicants were admitted (selected) by A and a total of 17 applicants were admitted (selected) by B.

2. Visualize this scenario: Given the above, it is possible that there is zero overlap between applicants admitted by A and B.

   1. i.e., given that there were a total of 40 applicants, it is possible that the 15 applicants admitted by A were different from the 17 applicants admitted by B.

   2. What this means is that it is possible that there are 0 applicants who were admitted by both A and B.

3. In this scenario, irrespective of who the 20 applicants admitted by C were,

   1. because there is not a single applicant admitted by both A and B,

   2. the number of applicants admitted by all 3 (A, B, and C) is 0.
      

4. Hence, the answer to the question asked (at the very least, how many applicants get the admission i.e., how many were admitted by all 3 interviewers) should be 0. This is the minimum possible value for the number of applicants admitted (selected) by all 3 interviewers.
   

The correct answer is choice A (0).

Need help visualizing the above? We don’t always have to use Venn diagrams. Here is a different way to visualize the scenario.

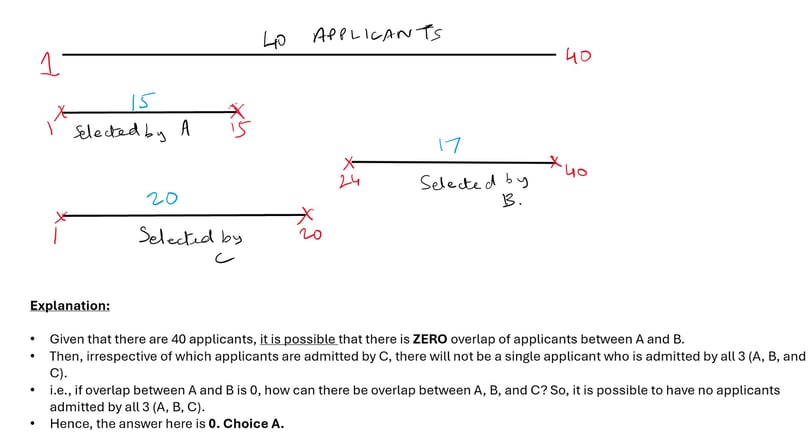
The first line shows the 40 candidates. Say, A selected candidate 1 to 15. It is possible that B selected candidates 24 to 40 (a completely different 17 people). Then, irrespective of who are the 20 people selected by C, it is impossible to have even a single applicant who got selected by all 3. Thus, the least possible number of such applicants is 0.

Hope this helps!
Harsha